【初心者向け】情報幾何学とは？｜AI分野への応用と数学的基礎を徹底解説

情報幾何学は統計学、情報理論、機械学習を結びつけAI技術を支える、数学的な枠組みです。

この記事では、情報幾何学の基礎から応用までを丁寧に解説します。

情報幾何学を学ぶことで複雑なデータ構造や確率分布を、幾何学的に捉えAI技術の発展に貢献できます。

AI研究者を目指す方は必見です。

この記事でわかること

• 情報幾何学の位置づけと重要性
• 情報幾何学の基礎概念（多様体、リーマン幾何学など）
• 機械学習、深層学習、データ分析への応用例
• 情報幾何学の学習方法とおすすめの参考書

情報幾何学の全体像

• 情報幾何学の位置づけ
• 情報幾何学の重要性
• 情報幾何学の魅力

情報幾何学は、統計学、情報理論、機械学習といった分野を結びつけ、AI技術において重要な役割を担う数学的な枠組みです。

この全体像を把握することで、個々の要素がどのように繋がり、応用されているかを理解できます。

情報幾何学は複雑なデータ構造や確率分布を幾何学的な視点から解析することを可能にし、AI分野に新たな視点をもたらします。

以下では、情報幾何学の位置づけ、重要性、魅力を解説します。

情報幾何学の位置づけ

情報幾何学は統計学、情報理論、機械学習といった関連分野と深く関わっています。

これらの分野を横断的に結びつけることで、それぞれの分野における課題解決に新たなアプローチをもたらし、相乗効果を生み出す役割を担います。

情報幾何学の重要性

情報幾何学の重要性は従来のユークリッド幾何学（※1）では捉えきれない、複雑なデータ構造や確率分布を扱える点にあります。

特に、高次元データや非線形な関係性を持つデータを解析する際に、情報幾何学はデータの構造をより深く理解し、新たな知見を得ることを可能にします。

※1 ユークリッド幾何学とは、古代ギリシャの数学者ユークリッドが体系化した幾何学で、平面上の図形を扱う数学の分野です。

情報幾何学の魅力

情報幾何学の魅力は、数式と図形が織りなす美しい理論体系にあります。

抽象的な概念を幾何学的なイメージとして捉えることで、直感的な理解を促し、新たな発想や問題解決の糸口を見つけやすくします。

以下は情報幾何学における「確率分布の空間（パラメータ空間）」の視覚的イメージです。

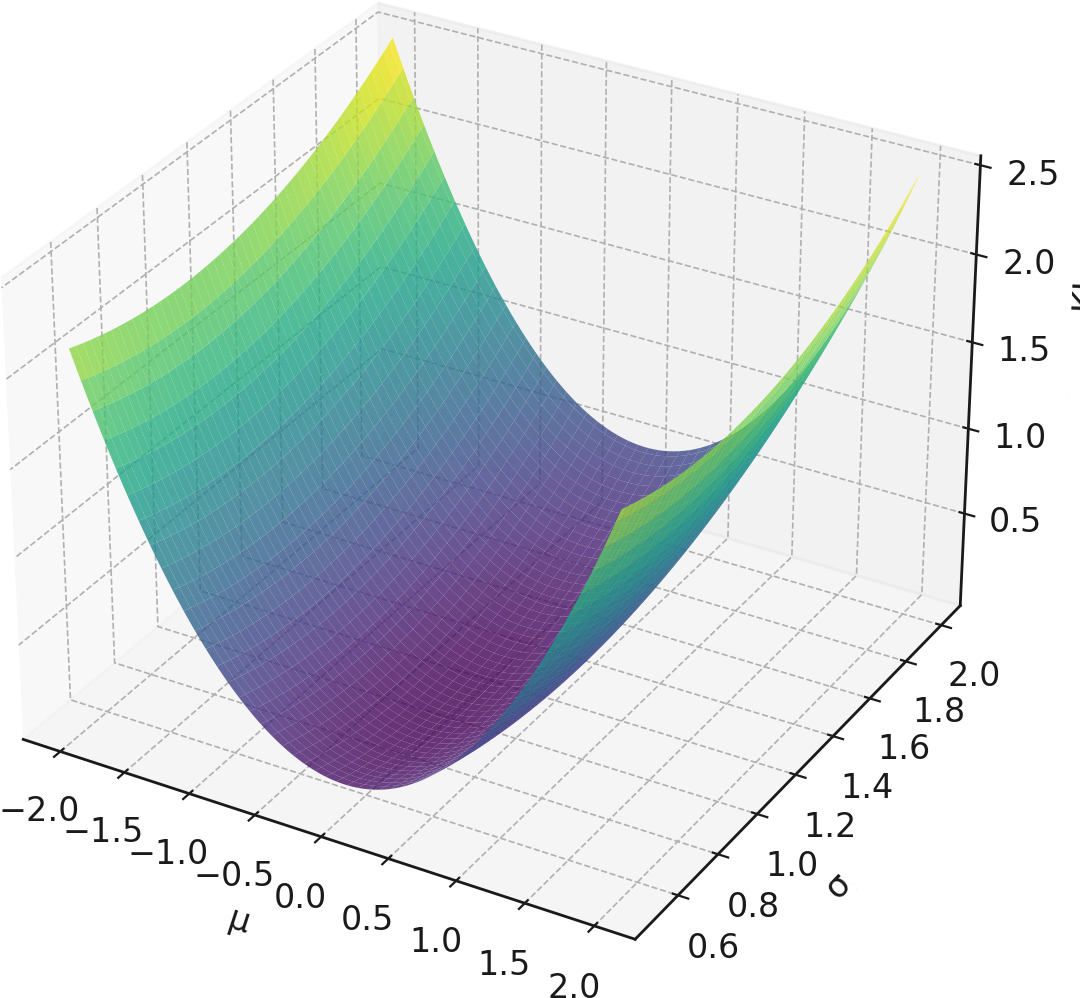
情報幾何学の基礎

• 多様体とは
• リーマン幾何学の基礎
• カルバック・ライブラー情報量について
• フィッシャー情報行列とは
• 自然勾配法と最適化の関係

情報幾何学は、統計学、情報理論、機械学習などを結びつけ、AI技術において重要な役割を担う数学的な枠組みです。

各見出しでは、多様体、リーマン幾何学、カルバック・ライブラー情報量、フィッシャー情報行列、自然勾配法といった、情報幾何学を理解する上で重要な要素を解説します。

情報幾何学の理解を深めることでAI技術の発展に貢献できます。

多様体とは

多様体とは局所的にはユークリッド空間と見なせるような空間のことで、高次元のデータや複雑な構造を持つデータを扱うための数学的な枠組みです。

多様体は、私たちが普段生活している3次元空間を一般化した概念です。

例えば、地球の表面は、局所的には平面として近似できますが、全体としては球面という多様体です。

このように多様体は曲がった空間や複雑な形状を持つ空間を、数学的に表現するための道具として利用できます。

多様体を用いることで、データの持つ本質的な構造を捉え、より高度な分析や機械学習が可能になります。

以下は情報幾何学における「多様体（鞍型曲面）」の視覚的イメージです。

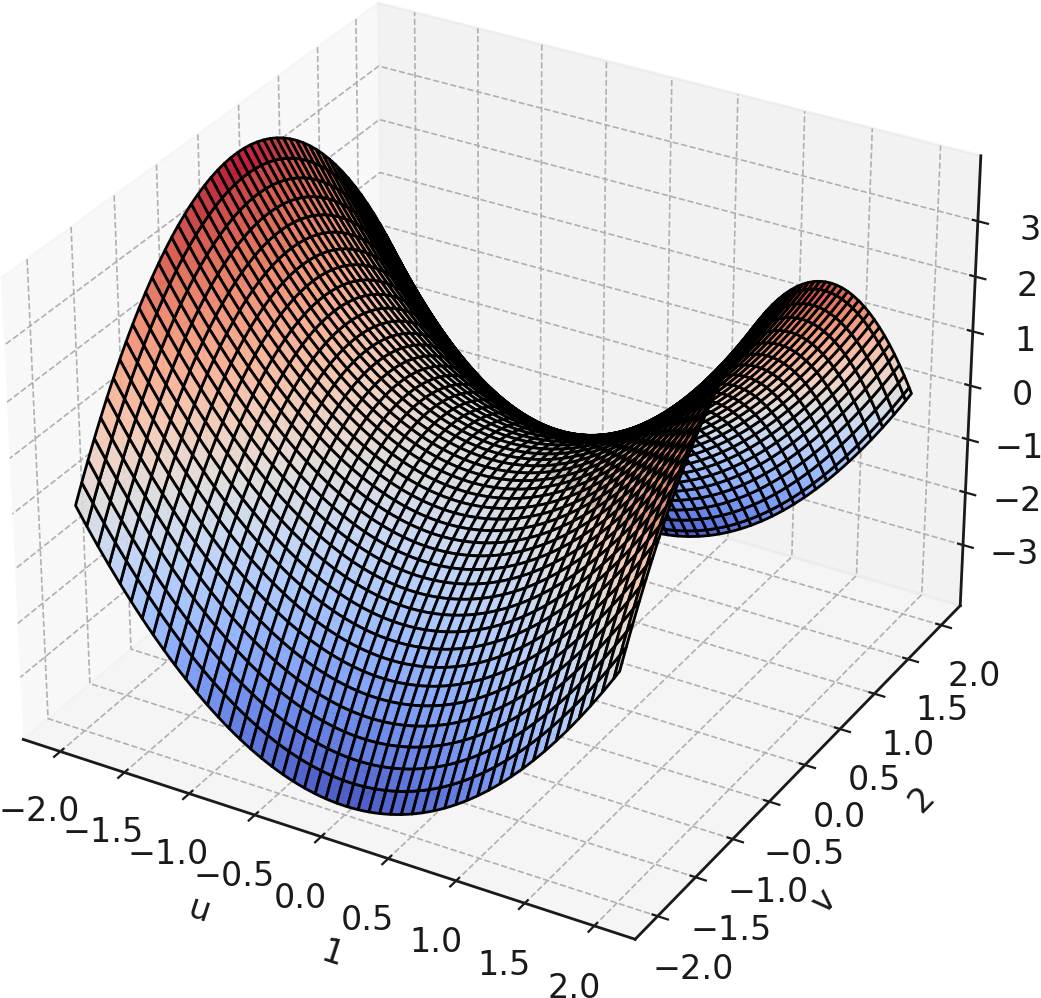
リーマン幾何学の基礎

リーマン幾何学は曲がった空間における幾何学であり、情報幾何学においては確率分布の空間を解析するための基礎となります。

リーマン幾何学では、空間の各点において、距離や角度を測るための計量という概念を導入します。

この計量を用いることで曲がった空間における最短距離（測地線）や角度を計算したり、空間の曲がり具合（曲率）を調べたりすることが可能です。

リーマン幾何学は、情報幾何学において、確率分布の空間を解析するための強力な道具であり、統計モデルの構造や性質を明らかにする上で重要な役割を果たします。

以下はリーマン幾何学における代表的な図の「2次元球面（S²）」の視覚的イメージです。

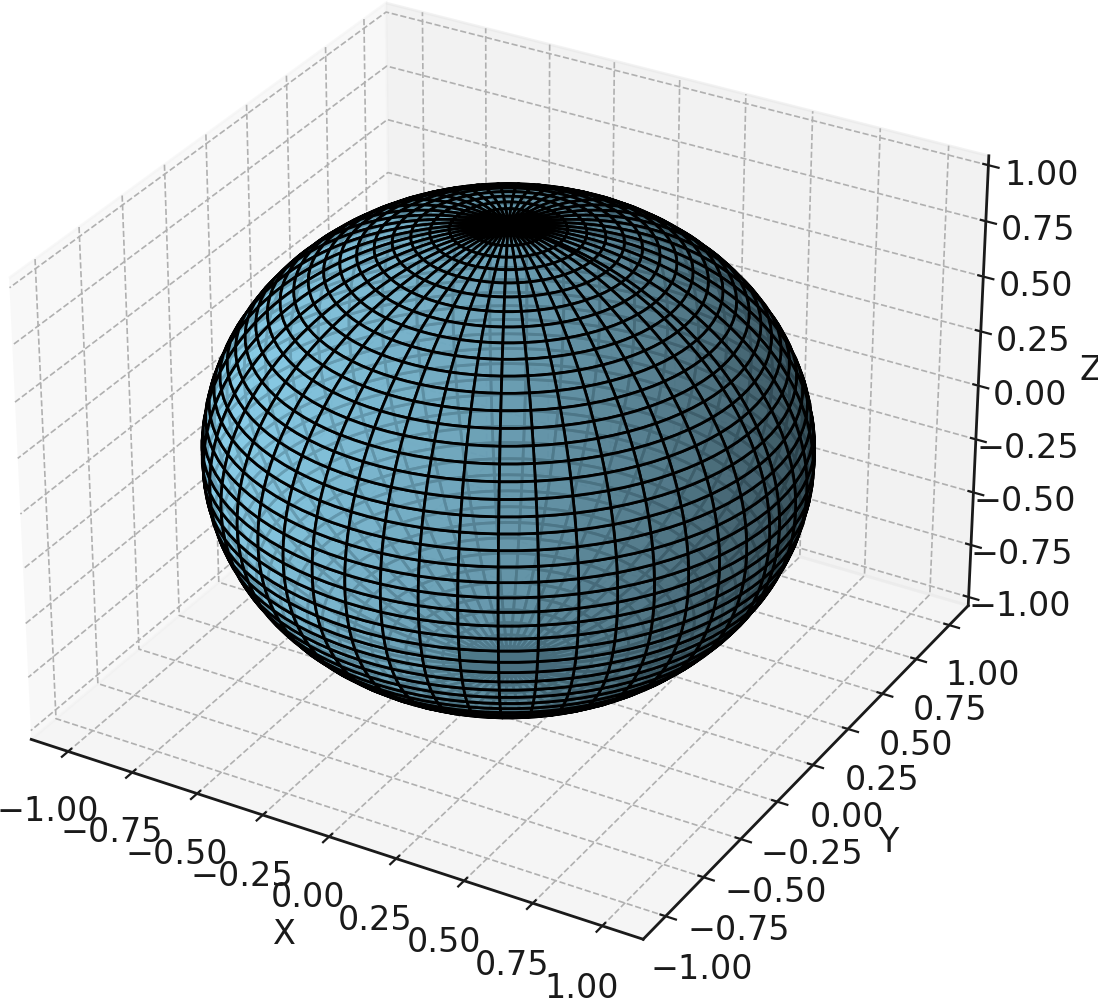
カルバック・ライブラー情報量について

カルバック・ライブラー情報量は2つの確率分布間の距離を測るための指標であり、情報幾何学において重要な役割を果たします。

カルバック・ライブラー情報量は、2つの確率分布がどれだけ異なっているかを定量的に評価するための尺度です。

ただし、カルバック・ライブラー情報量は厳密には距離の公理を満たさないため、確率分布間の「ダイバージェンス（※2）」と呼ばれることがあります。

カルバック・ライブラー情報量を用いることで、確率分布間の微妙な違いを捉え、より高度なデータ分析や機械学習が可能になります。

以下はカルバック・ライブラー情報量の視覚的イメージです。

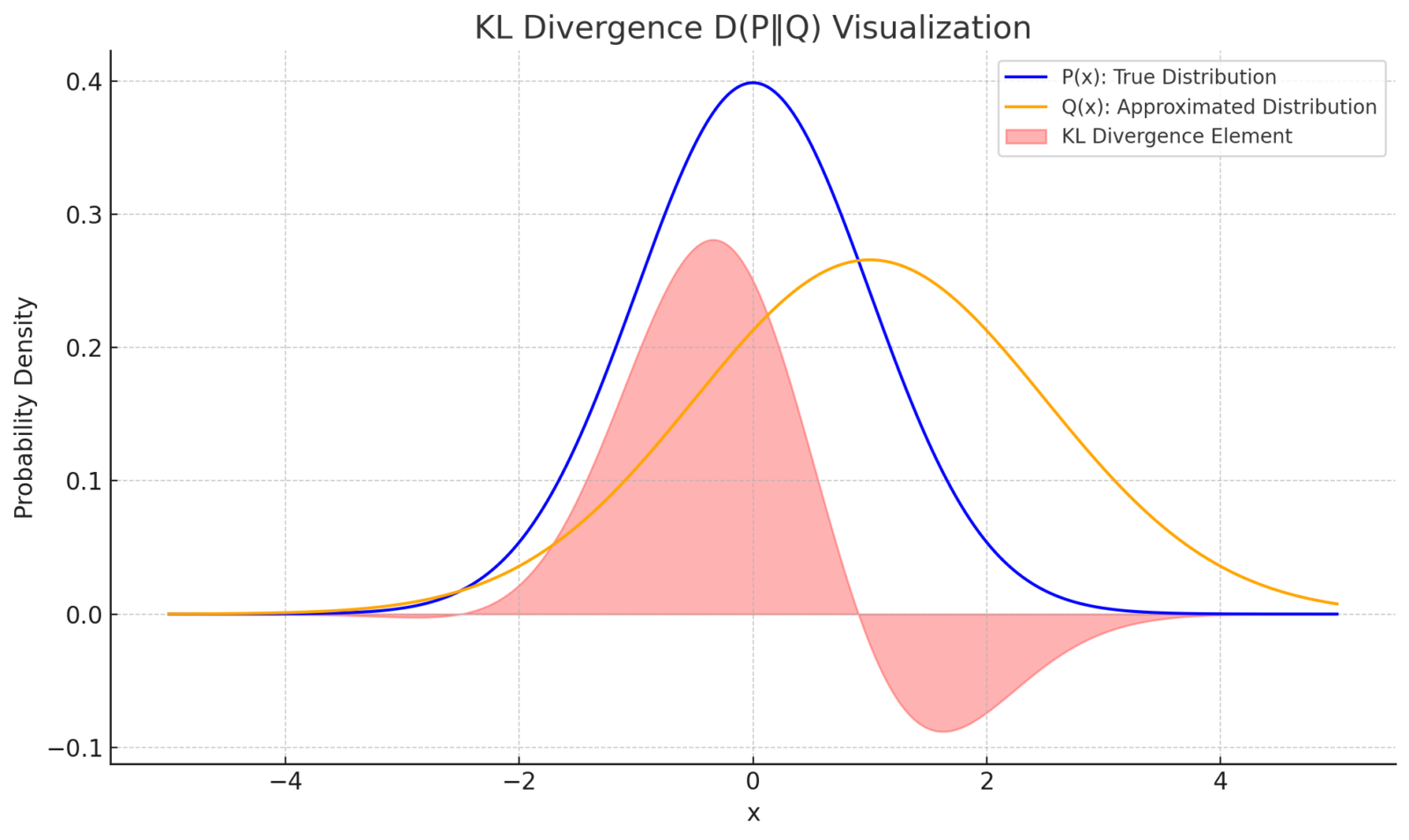
※2 ダイバージェンスとは、2つのもの（特に確率分布など）が「どれだけ違うか」を表す尺度のことです。ただし、普通の「距離」とは違い、「AからBへの違い と BからAへの違い が異なる（非対称である）」ことが多いのが大きな特徴です。

フィッシャー情報行列とは

フィッシャー情報行列は、統計モデルにおけるパラメータ推定の「精度」や「不確かさ」を測るための重要な指標であり、情報幾何学において重要な役割を果たします。

フィッシャー情報行列の固有値が大きいほど、パラメータの推定精度が高いことを意味します。

項目	説明
役割	パラメータの推定精度の測定
特徴	フィッシャー情報行列の固有値が大きいほど推定精度が高い
情報幾何学との関連	統計モデルのパラメータ空間における「内積」や「距離」を定義する行列（＝リーマン計量）

フィッシャー情報行列を用いることで、統計モデルのパラメータ空間の幾何構造を理解し、より効率的なパラメータ推定やモデル設計が可能になります。

以下は正規分布 N(μ, σ²) におけるフィッシャー情報量の図です。

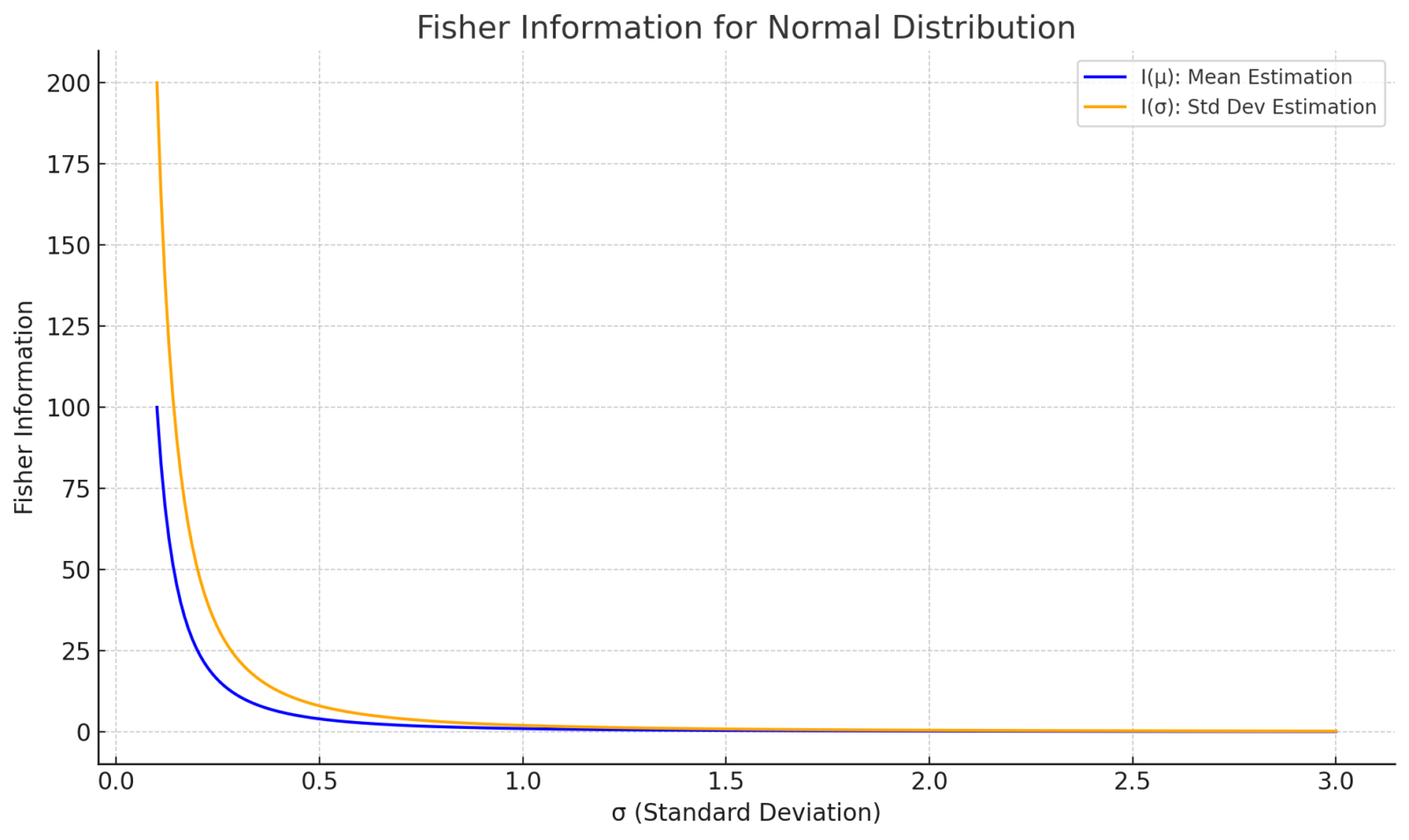
自然勾配法と最適化の関係

自然勾配法は情報幾何学の考え方を応用した最適化アルゴリズムであり、機械学習モデルの学習効率を向上させる効果があります。

自然勾配法は、パラメータ空間の歪みを考慮することで、従来の勾配法よりも効率的な学習を可能にします。

特に高次元のパラメータ空間や複雑な構造を持つモデルにおいて、その効果を発揮します。

自然勾配法を用いることで、機械学習モデルの学習を効率化し、より高性能なモデルを開発することが可能になります。

以下は通常の勾配法と自然勾配法の違いを示すイメージです。

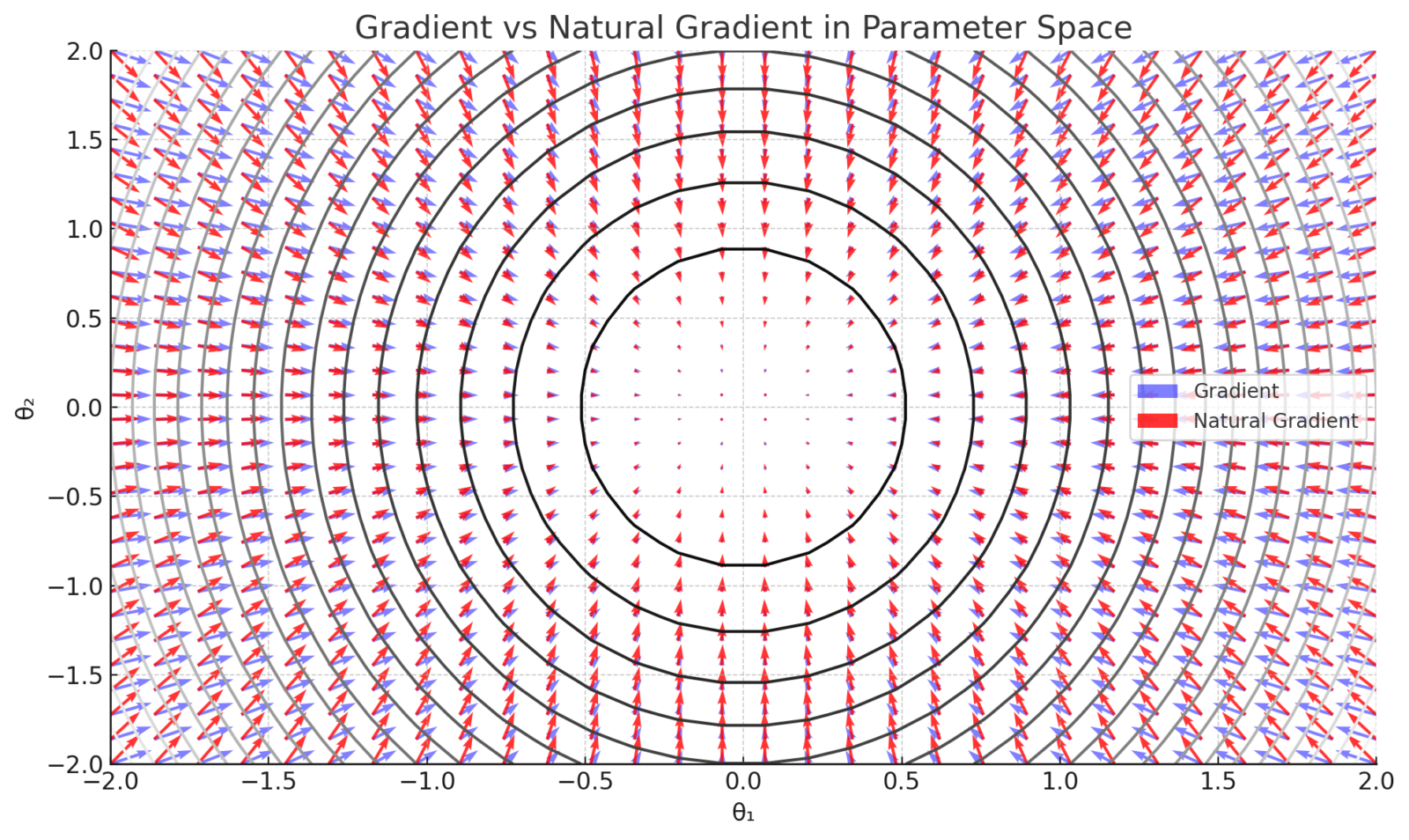
グレーの等高線：損失関数（例：凸な二次関数）の値（低いほどよい）
青い矢印：通常の勾配法（Gradient Descent）の方向 → ユークリッド空間における最急降下方向
赤い矢印：自然勾配法（Natural Gradient Descent）の方向 → フィッシャー情報行列によって歪みを補正した最適方向

情報幾何学の応用

• 機械学習での応用例
• 深層学習における活用
• データ分析への展開
• 脳科学への応用
• 金融工学への応用
• 自然言語処理への応用

情報幾何学の応用は多岐にわたりますが、特に重要なのはその理論が、機械学習・深層学習・データ分析・脳科学・金融工学・自然言語処理といった広範な分野に、革新的な視点をもたらしている点です。

これらの分野では情報幾何学の概念や手法を活用することで、従来の手法では困難だった問題の解決や新たな知見の発見が期待されています。

ここでは、各応用例の概要について記述します。

それぞれの応用例が情報幾何学の理論をどのように活用し、具体的な問題解決に貢献しているのか、詳細を見ていきましょう。

機械学習での応用例

機械学習において情報幾何学はモデルの学習過程や性能評価を最適化するための、強力なツールとして利用されています。

特にパラメータ空間の幾何学的構造を考慮することで、学習効率の向上や汎化性能の改善が期待できます。

情報幾何学が機械学習にもたらす具体的な利点は、以下の通りです。

利点	詳細
自然勾配法	パラメータ空間の歪みを考慮した最適化アルゴリズム
モデルの正則化	過学習を抑制し、汎化性能を向上
モデル選択	情報量基準に基づいた最適なモデル選択

機械学習における情報幾何学の応用は、モデルの性能向上だけでなく、解釈性の向上にも貢献します。

パラメータ空間の幾何学的構造を理解することで、モデルの挙動や学習過程に関する新たな洞察を得ることができます。

深層学習における活用

深層学習の分野では情報幾何学がモデルの学習過程の安定化や、内部表現の解釈に役立っています。

深層学習モデルはその複雑さから学習が困難になることがありますが、情報幾何学的なアプローチを用いることで、より効率的かつ安定した学習が期待できます。

深層学習における情報幾何学の活用例を以下に示します。

活用例	詳細
学習率の調整	パラメータ空間の曲率を考慮した適応的な学習率調整
内部表現の可視化	高次元な内部表現を低次元空間に埋め込み、可視化
モデルの解釈	モデルの学習過程や意思決定に関する洞察を獲得

深層学習における情報幾何学の応用は、モデルの性能向上だけでなく、ブラックボックス化しやすい深層学習モデルの解釈を支援し、信頼性の高いAIシステムの開発に貢献します。

データ分析への展開

データ分析において情報幾何学はデータの持つ複雑な構造を明らかにし、より高度な分析を可能にするためのツールとして活用されています。

特に高次元データや非線形な関係性を持つデータの分析において、その有効性が期待されています。

データ分析における情報幾何学の応用例としては、以下のようなものが挙げられます。

応用例	詳細
次元削減	高次元データを低次元空間に効率的に埋め込み、可視化
クラスタリング	データの幾何学的構造に基づいた高精度なクラスタリング
異常検知	データ空間における異常なデータの検出

データ分析における情報幾何学の応用は、従来の手法では捉えきれなかったデータの潜在的な構造を明らかにし、新たな知見の発見や問題解決に貢献します。

脳科学への応用

脳科学では情報幾何学が脳の神経活動や情報処理のメカニズムを理解するための新たな視点を提供しています。

脳は非常に複雑なシステムであり、その動作原理を解明するためには高度な数学的ツールが不可欠です。

情報幾何学は、脳の神経活動を幾何学的な構造として捉え、その複雑さを解析するための強力な手段となります。

脳科学における情報幾何学の具体的な応用例を以下に示します。

応用例	詳細
脳波解析	脳波のパターンを幾何学的に解析し、精神状態や認知機能を評価
神経回路モデル	神経回路の構造を情報幾何学的にモデル化し、情報伝達のメカニズムを解明
脳の可塑性	脳の構造変化を情報幾何学的に解析し、学習や記憶のメカニズムを理解

脳科学における情報幾何学の応用は、脳の動作原理の解明だけでなく、精神疾患の診断や治療法の開発にも貢献する可能性があります。

金融工学への応用

金融工学において情報幾何学は金融市場の変動やリスク管理に役立てられています。

金融市場は様々な要因が複雑に絡み合って変動するため、その解析には高度な数学的スキルが求められます。

情報幾何学は、金融市場のデータを幾何学的な構造として捉え、リスクの評価や予測に役立てることができます。

金融工学における情報幾何学の活用例としては、以下のようなものが挙げられます。

活用例	詳細
ポートフォリオ最適化	リスクとリターンのバランスを考慮した最適なポートフォリオ構築
デリバティブ評価	複雑な金融商品の価格を幾何学的に評価
リスク管理	金融市場のリスクを幾何学的に評価し、適切なリスクヘッジ戦略を策定

金融工学における情報幾何学の応用は、より高度な金融商品の開発や、リスク管理の効率化に貢献し、金融市場の安定化に寄与することが期待されます。

自然言語処理への応用

自然言語処理（NLP）（※4）の分野では情報幾何学が言語データの構造解析や、言語モデルの性能向上に貢献しています。

言語データはその複雑さから解析が難しいとされていますが、情報幾何学的なアプローチを用いることで、言語の潜在的な構造を明らかにすることができます。

自然言語処理における情報幾何学の具体的な応用例を以下に示します。

応用例	詳細
単語の分散表現	単語の意味を幾何学的なベクトルとして表現し、単語間の関係性を解析
文章の構造解析	文章の構造を幾何学的に解析し、文章の意図や意味を抽出
言語モデルの最適化	言語モデルのパラメータ空間を情報幾何学的に解析し、モデルの性能を向上

自然言語処理における情報幾何学の応用は、機械翻訳や文章要約といったタスクの性能向上だけでなく、人間の言語理解のメカニズム解明にも貢献する可能性があります。

※4 自然言語処理（NLP）とは、人間の言葉（自然言語）を機械で処理して意味を解析する技術です。

情報幾何学を学ぶ

• 情報幾何学の参考書紹介
• 情報幾何学の学習方法
• 情報幾何学の研究動向
• 情報幾何学関連のイベント・セミナー
• 情報幾何学の勉強における注意点

情報幾何学を学ぶことはAI技術の最前線を理解し、より高度なAIシステムを開発するために必要不可欠です。

情報幾何学を学ぶことで統計学、情報理論、機械学習といった分野を横断的に結びつけ、複雑なデータ構造や確率分布を幾何学的な視点から解析できるようになり、AI研究者としてのスキルアップに繋がります。

ここでは、情報幾何学を学ぶための参考書、学習方法、研究動向、イベント・セミナー、勉強における注意点について解説します。

情報幾何学の参考書紹介

情報幾何学を学ぶ上で、自分に合った参考書を選ぶことは非常に重要です。

基礎をしっかりと理解できる入門書から、より専門的な内容を扱った発展書まで、様々なレベルの参考書があります。

自分の現在の知識レベルや学習目的に合わせて、適切な参考書を選びましょう。

書籍名	著者	特徴	おすすめの読者
情報幾何学の基礎	甘利俊一	情報幾何学の入門書として最適。数式展開も丁寧で、初学者でも理解しやすい。	情報幾何学を初めて学ぶ人
統計的学習の基礎	Trevor Hastie, Robert Tibshirani, Jerome Friedman	機械学習の理論的な背景を学ぶ上で必携。情報幾何学との関連も深い。	機械学習の理論を深く理解したい人
パターン認識と機械学習	Christopher Bishop	ベイズ的な視点から機械学習を解説。情報幾何学の応用例も紹介されている。	機械学習の応用を学びたい人

情報幾何学の学習方法

情報幾何学は数学的な知識を必要とする分野なので、段階的に学習を進めていくことが重要です。

まずは、情報幾何学の基礎となる微分幾何学や統計学の知識を習得し、その後、情報幾何学の専門書や論文を読むと良いでしょう。

また実際に手を動かして計算したり、プログラムを書いてみたりすることも、理解を深める上で役立ちます。

情報幾何学の効果的な学習方法：

1. 基礎知識の習得: 微分幾何学、線形代数、統計学の基礎を固める
2. 参考書を読む: 入門書から始めて徐々にレベルアップ
3. 数式を理解する: 数式の意味を理解し、自分で導出してみる
4. プログラムを実装する: 理論を実装し、動作を確認する
5. 論文を読む: 最新の研究動向を把握する

情報幾何学の研究動向

情報幾何学の研究は機械学習やAI分野の発展とともに、ますます活発化しています。

近年では、深層学習モデルの解釈や最適化、生成モデルの学習、強化学習など、様々な分野への応用が試みられています。

また情報幾何学の理論的な発展も進んでおり、新しい概念や手法が次々と生まれています。

情報幾何学の研究動向：

研究分野	内容
深層学習	深層学習モデルの解釈、最適化、汎化性能の向上
生成モデル	生成モデルの学習、GANの安定化、VAEの改善
強化学習	強化学習における探索、報酬設計、方策勾配法の改善
統計的推論	ベイズ推論、変分推論、EMアルゴリズムの改善
データ可視化	高次元データの可視化、次元削減、特徴抽出

情報幾何学関連のイベント・セミナー

情報幾何学に関する知識を深めるためにはイベントやセミナーに参加することも有効です。

これらのイベントでは、最先端の研究に触れたり、研究者やエンジニアと交流したりすることができます。

またハンズオン形式のセミナーでは実際にプログラムを動かしながら、情報幾何学の応用を学ぶことができます。

情報幾何学関連のイベント・セミナー例：

イベント名	内容	参加対象者
情報幾何学ワークショップ	情報幾何学の基礎から応用までを学ぶ	学生、研究者、エンジニア
機械学習セミナー	機械学習における情報幾何学の応用事例を紹介	機械学習エンジニア、データサイエンティスト
国際会議 (例: NeurIPS, ICML, ICLR)	情報幾何学に関する最新の研究発表が行われる	研究者、学生

情報幾何学の勉強における注意点

情報幾何学の勉強は数学的な基礎知識が必要となるため、容易ではありません。

しかし焦らずに一つずつ理解していくことで、必ず習得できます。

重要なことは、継続することと、疑問点を放置しないことです。

難しいと感じたら、基礎的な参考書に戻ったり、詳しい人に質問したりするなどして、着実に理解を深めていきましょう。

情報幾何学の勉強における注意点：

1. 基礎知識を疎かにしない: 微分積分、線形代数、確率統計の基礎をしっかりと理解する
2. 焦らずに一つずつ理解する: 難しい概念は、時間をかけて丁寧に理解する
3. 疑問点を放置しない: 分からないことは、すぐに質問する
4. 継続する: 諦めずに、毎日少しずつでも学習を続ける
5. 実践する: 実際に手を動かして計算したり、プログラムを書いてみたりする

よくある質問（FAQ）

まとめ

情報幾何学は、統計学、情報理論、機械学習を結びつけ、AI技術を支える数学的な枠組みです。

この記事では、情報幾何学の基礎から応用までをできるだけ分かりやすく解説してみました。

• 情報幾何学の位置づけと重要性
• 情報幾何学の基礎概念（多様体、リーマン幾何学など）
• 機械学習、深層学習、データ分析への応用例

情報幾何学を学ぶことで、複雑なデータ構造や確率分布を幾何学的に捉え、AI技術の革新に貢献できます。

AI研究者を目指す方は、ぜひ情報幾何学の世界へ足を踏み入れてみてください。